It is, of course, impossible to determine exactly what the world’s most difficult and most famous mathematical problem is. However, the Riemann Hypothesis, which has baffled mathematicians since it was proposed by Bernhard Riemann in 1859, seems to be a candidate. The Riemann Hypothesis is the eighth problem on David Hilbert’s list of 23 unsolved problems published in 1900. It is also the second most important problem in the Clay Mathematics Institute Millennium Prize Problems (2000). The person who solves this hypothesis will of course go down in history. However, since it is one of the “Million Dollar Problems”, it will also eliminate financial difficulties.
- Health Officials in New York Issue a Warning That Hundreds Could Become Infected For Every Case of Polio
- The FBI raided Donald Trump’s home in Florida!
The Riemann hypothesis is essentially about prime numbers, but rather about the distribution of prime numbers on the number line. Mathematicians study the properties of primes because of their interest in the subject. But primes also have modern scientific applications, especially in cryptography.
As the name suggests, it is only a conjecture for now, but a solution to the Riemann hypothesis will prove hundreds of other theorems. It will determine that certain algorithms will run in a relatively short time and explain the distribution of gaps between primes. At this point, we may have to rethink our security.

What is the Riemann hypothesis in a nutshell?
To understand what the Riemann hypothesis is, we need to start with what prime numbers are. You may remember your elementary school math teacher defining them as numbers divisible only by themselves and one. This is true, but that’s not all. For a mathematician, primes are like atoms, the building blocks of every number. When we have small numbers, we can find these building blocks by factorization. But as the numbers get bigger, this becomes more difficult. Also, once we find a prime number, we don’t know where the next prime number will be. This is why mathematicians look at the distribution of primes.
In the late eighteenth century, two legendary mathematicians, Carl Friedrich Gauss and Adrien-Marie Legendre, began to study primes independently of each other. Could prime numbers appear in a certain order, like the elements in the Periodic Table? This was the question on their minds. The primes are irregularly distributed on the number line. The larger the numbers, the more sparsely the primes appear. The prime number theorem gives us the number of primes less than or equal to any given positive real number. In other words, given a positive integer n, it tells us how many integers up to and including n are prime numbers. (See this article for details)
In the 1700s, Leonhard Euler succeeded in defining the zeta function. This function, denoted by the sixth letter of the Greek alphabet zeta (ζ), was of the form ζ(s) = 1 + 2-s + 3-s + 4-s +…. Euler showed that the zeta function is equal to an infinite product. The terms of this infinite product were prime numbers. (See this article for more.) However, the zeta function defined by Euler was only valid for values of s greater than 1.
Riemann Zeta Function
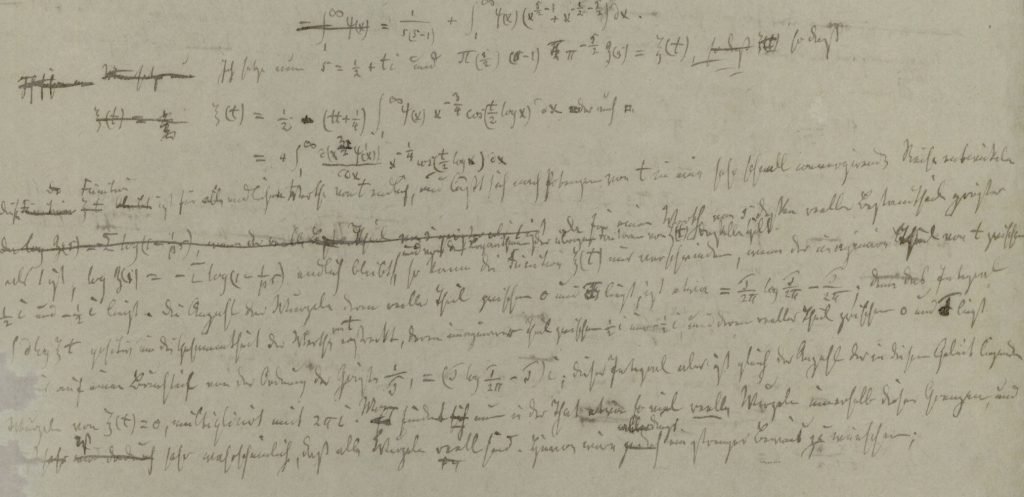
In 1859, the German mathematician Bernhard Riemann (1826-1866) presented a paper entitled “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse” to the Berlin Academy. In fact, this was his only paper on number theory. In this paper, Riemann found a function for values greater than 1 that was identical to Euler’s zeta function, but better defined. He took Euler’s zeta function and extended it to include complex numbers. In this new form, the function is known as the Riemann zeta function.
Estimating how many primes there are up to a given number depends on knowing for which values the Riemann zeta function is zero. The function goes to zero for all negative even integers (-2, -4, -6, etc.). But these are not relevant to solving the problem of how prime numbers are distributed. They are therefore called trivial zeros. There are also infinitely many values that make the function zero in the critical region between x= 0 and x=1. The biggest unsolved problem in the history of mathematics, now called the Riemann hypothesis, is whether all of these values lie on the x=1/2 line in the complex plane.
Riemann himself made the first checks by hand to make sure they obeyed the rule. In 1986 it was verified that one and a half billion zeros of the Riemann zeta function lie on the x=1/2 line. After running ZetaGrid, the first 100 billion zeros of the Riemann function were found to lie on this line without exception.
Why is the Riemann Hypothesis Important?
The Riemann Hypothesis arises very often in seemingly unrelated fields other than prime numbers. Therefore, the importance of proving (or disproving) it goes far beyond the boundaries of number theory or mathematics as a whole. The Riemann hypothesis has a subtle but direct connection to the subatomic universe. In nuclear physics, the pattern in the distribution of zeros of the Riemann zeta function is exactly the same as the pattern in the distribution of energy levels of a heavy atom, the uranium atom. This could mean that quantum mechanics is linked to prime numbers. This is a crazy idea in itself. This is why the Riemann hypothesis is important in that it connects seemingly unrelated topics in mathematics. Among the trillions of computer-controlled zeros, no exceptions were found. They all fell within the critical line predicted by Riemann.

